Calculus Product and Quotient Rule

Quotient Rule Derivative: The quotient rule formula may be a little difficult to remember. Perhaps a little yodeling-type chant can help you. Imagine a frog yodeling, ‘LO dHI less HI dLO over LO LO.’ In this mnemonic device, LO refers to the denominator function and HI refers to the numerator function.

Derivative Quotient Rule

If you have function f(x) in the numerator and the function g(x) in the denominator, then the derivative is found using this formula:

In this formula, the d denotes a derivative. So, df(x) means the derivative of function f and dg(x) means the derivative of function g. The formula states that to find the derivative of f(x) divided by g(x), you must:

1. Take g(x) times the derivative of f(x).
2. Then from that product, you must subtract the product of f(x) times the derivative of g(x).
3. Finally, you divide those terms by g(x) squared.

The quotient rule formula may be a little difficult to remember. Perhaps a little yodeling-type chant can help you. Imagine a frog yodeling, ‘LO dHI less HI dLO over LO LO.’ In this mnemonic device, LO refers to the denominator function and HI refers to the numerator function.

Let’s translate the frog’s yodel back into the formula for the quotient rule.

LO dHI means denominator times the derivative of the numerator: g(x) times df(x).

less means ‘minus’.

HI dLO means numerator times the derivative of the denominator: f(x) times dg(x).

over means ‘divide by’.

LO LO means take the denominator times itself: g(x) squared.

Quotient Derivative Rule

In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions.^[1][2][3] Let {\displaystyle f(x)=g(x)/h(x),} where both {\displaystyle g} and {\displaystyle h} are differentiable and {\displaystyle h(x)\neq 0.} The quotient rule states that the derivative of {\displaystyle f(x)} is

                                                   

Quotient Rule Derivative Formula

The following problems require the use of the quotient rule. In the following discussion and solutions the derivative of a function h(x) will be denoted by  or h‘(x) . The quotient rule is a formal rule for differentiating problems where one function is divided by another. It follows from the limit definition of derivative and is given by

 .

Remember the rule in the following way. Always start with the “bottom” function and end with the “bottom” function squared. Note that the numerator of the quotient rule is identical to the ordinary product rule except that subtraction replaces addition. In the list of problems which follows, most problems are average and a few are somewhat challenging.

• PROBLEM 1 : Differentiate  .

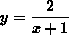Click HERE to see a detailed solution to problem 1.

• PROBLEM 2 : Differentiate  .

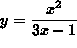Click HERE to see a detailed solution to problem 2.

• PROBLEM 3 : Differentiate  .

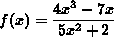Click HERE to see a detailed solution to problem 3.

• PROBLEM 4 : Differentiate  .

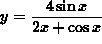Click HERE to see a detailed solution to problem 4.

• PROBLEM 5 : Differentiate  .

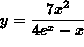Click HERE to see a detailed solution to problem 5.

• PROBLEM 6 : Differentiate  .
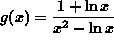• Click HERE to see a detailed solution to problem 6
• PROBLEM 7 : Differentiate  .

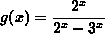Derivative Product And Quotient Rule

We can build new functions from old ones by forming quotients.

• Quotient: f/g

Given functions f and g with target sets consisting of real numbers, the quotient of f and g is the new function f/g defined as follows.

(f/g)(x) = f(x)/g(x)
We must be a little careful in determining the domain of the quotient f/g: a real number x lies in the domain of f/g if and only if it is in the domain of both f and g AND g(x) is not equal to zero. Division by zero is never allowed. Not now. Not ever.

A special type of quotient is the reciprocal of a function.

• Reciprocal: 1/g

The domain of the reciprocal is the set of all points x in the domain of g for which g(x) is not zero.

Example. The cosecant function is the reciprocal of the sine function.

csc(x) = 1/sin(x)
Example. Power functions with negative exponents also arise as reciprocals.

x ^-n = 1/xⁿ